Jak analiza regresji może zwiększyć efektywność normowania czasu pracy?

Jedną z najbardziej rozpowszechnionych metod ustalania norm czasu pracy jest chronometraż. Norma zostaje określona po przeprowadzeniu szeregu pomiarów czasu wykonywania danej pracy. Czy zatem, jeśli w przedsiębiorstwie bazujemy na chronometrażu, musimy zawsze przeprowadzać pomiary czasu dla uzyskania normy dla określonego wyrobu? Otóż nie. Wystarczy, po spełnieniu pewnych warunków, skorzystać z instrumentarium analizy regresji. Dzięki niemu będziemy mogli wykorzystać pomiary wykonane dla aktualnie produkowanych wyrobów do ustalania norm dla wyrobów wchodzących do produkcji w przyszłości.

Krótkie przypomnienie – czym jest regresja i po co się ją analizuje?

Mówiąc uczenie, za internetowym wydaniem encyklopedii PWN, regresja to „statyst. zależność zmiennej losowej Y od zmiennych losowych X₁, X₂, … , X_n”. Mówiąc bardziej potocznie – analizując regresję szukamy i badamy zależności między różnymi wielkościami, usiłując stworzyć model tych zależności, np. w postaci funkcji matematycznej. Zakładamy przy tym, że jedna z wielkości zależy od jednej lub większej ilości innych. W ten sposób możemy badać np. zależność pomiędzy poziomem wykształcenia ludzi a poziomem dochodów w rodzinach, z których pochodzą i miejscem zamieszkania tych rodzin. Wielkość, która, jak sądzimy, zależy od innych, nazywana jest wielkością (zmienną) objaśnianą. Wielkości, od których zależy wielkość objaśniana, to wielkości (zmienne) objaśniające. W przytoczonym przykładzie badalibyśmy zatem, czy poziom zamożności rodziny i miejsce jej zamieszkania objaśnia poziom wykształcenia dzieci.

Modele tworzone w analizie regresji możemy wykorzystać nie tylko do opisu rzeczywistości ale także do przewidywania wartości wielkości objaśnianej w zależności od wartości wielkości objaśniającej (lub wielkości objaśniających). Rozpatrzmy następujący, bardzo uproszczony, przykład: zmierzono, że ręczne pomalowanie farbą elementu o powierzchni 0,5 m² zajmuje 30 sekund, elementu o powierzchni 0,75 m² 50 sekund, a elementu o powierzchni 1 m², taką samą farbą, w takich samych warunkach, trwa 70 sekund. Intuicja podpowiada nam, że czas potrzebny na pomalowanie elementu będzie zależał od jego powierzchni . Odnosząc się do użytej wcześniej terminologii czas byłby tu wielkością objaśnianą, a powierzchnia elementu wielkością objaśniającą. Po naniesieniu uzyskanych z pomiarów danych na układ współrzędnych i połączeniu ich linią, otrzymalibyśmy poniższy wykres

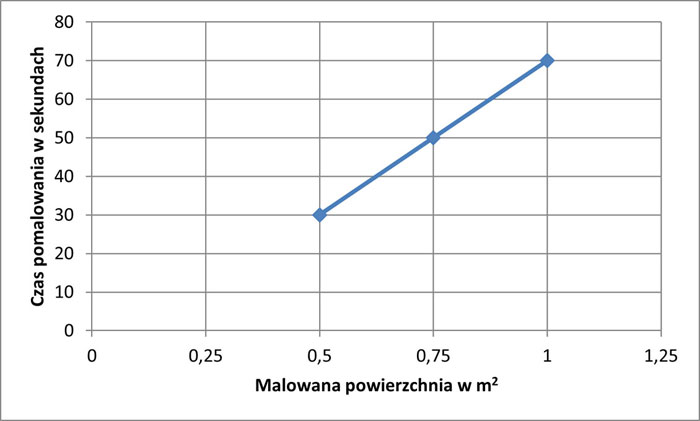
Przyjmując czas za y, a powierzchnię za x możemy określić równanie prostej, której odcinek widnieje na wykresie. Będzie ono miało postać:

y = 80x-10

Nasze równanie (model opisujący zależność wielkości od siebie) powstał na podstawie dostępnych danych z dokonanych pomiarów czasu. Możemy go użyć do predykcji, przewidzenia, ile czasu będzie trwało pomalowanie określonej powierzchni bez konieczności dokonywania pomiarów, oczywiście zakładając, że żaden z innych elementów (rodzaj farby, rodzaj podłoża itp. nie ulegną zmianie). Podstawiając za x 0,8 (m²) otrzymamy dla y wynik 54 (sekundy). Aby go uzyskać nie musieliśmy dokonywać pomiarów, wystarczyło podstawić dane do wzoru.

Ważna uwaga – pamiętajmy, że nasz model określiliśmy na podstawie danych z przedziału o granicach 0,5 m² i 1 m². Analizując uzyskane dane stwierdziliśmy zależność liniową pomiędzy czasem a powierzchną i założyliśmy, że taka zależność występuje dla wszystkich punktów w tym przedziale. Mogliśmy zatem „w miarę bezpiecznie” użyć modelu do predykcji czasu dla wartości powierzchni leżącej w granicach przedziału . Użycie go dla wartości spoza przedziału byłoby niczym nie uzasadnionym „gdybaniem”, ekstrapolacją. Nie znamy, nie mamy danych na temat przebiegu funkcji poza granicami przedziału. „Gdybanie” może być bardzo ryzykowne. Łatwo się o tym przekonać, usiłując zastosować nasz model do predykcji czasu potrzebnego na pomalowanie powierzchni 0,1 m².

Świat nie jest idealny, czyli regresja w praktyce.

W praktyce nie należy się raczej liczyć z tym, że zmierzone czasy danej pracy, przy przyjęciu jednej lub więcej zmiennych objaśniających, będą się zawsze idealnie układały na jakiejś prostej (czy krzywej, o czym później). A chcielibyśmy, podobnie jak w poprzednim przypadku, uzyskiwać wzory, które można by stosować do prognozowania. Jest to możliwe. Aby to pokazać skomplikujmy nieco nasz przykład. Załóżmy, że przeprowadzono serię pomiarów czasu potrzebnego na pomalowanie różnej wielkości powierzchni w przedziale od 0,5m² do 1m². Wyniki zebrano w poniższej tabeli.

	Powierzchnia malowania w m2
	0,5	0,6	0,7	0,8	0,9	1,0
Czas w sekundach	29	39	43	55	60	70

Nanieśmy te dane na układ współrzędnych.

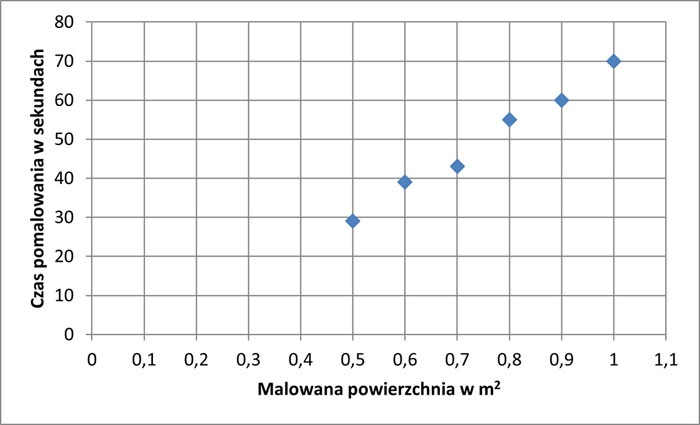
Widzimy, że teraz nie da się wykreślić prostej, na której leżałyby wszystkie punkty wynikające z przeprowadzonych pomiarów czasu. Co prawda punkty wyraźnie nie leżą na jednej prostej ale ich układ zachęca nas do próby znalezienia jakiejś „prostej kompromisowej”, będącej najlepszym możliwym przybliżeniem „prostej idealnej”. Możemy w tym celu skorzystać choćby z funkcji REGLINP programu Microsoft® Office Excel®. Dzięki temu uzyskamy równanie „prostej kompromisowej” w postaci:

y = 80x -10,6667

W jaki sposób zostało uzyskane to równanie i co oznacza „prosta kompromisowa”? Funkcja REGLINP stosuje metodę najmniejszych kwadratów. Na czym ona polega? Spójrzmy na poniższy wykres (są na nim te same punkty z pomiarów co na poprzednim wykresie, dla większej przejrzystości zmienione są tylko współrzędne osi).

Pomiędzy wartościami czasu z pomiarów, a prostą wytyczoną przez funkcję REGLINP widać większe lub mniejsze odchylenia. Na wykresie zaznaczono jedno z tych odchyleń (dla czasu zmierzonego dla pomalowania powierzchni 0,7m²). Prosta została wytyczona w taki sposób, aby dla wszystkich punktów z pomiarów suma kwadratów ich odchyleń od prostej była najmniejsza z możliwych. Innymi słowy, gdyby prostą wykreślić jakkolwiek inaczej to suma kwadratów odchyleń byłaby większa. Prosta nie jest „idealna”, nie przechodzi przez wszystkie punkty z pomiarów czasu, daje jednak możliwość prognozowania. Możemy za jej pomocą obliczyć np. czas na pomalowanie powierzchni 0,75m² (wynik wyniesie 49,33 sekundy). Oczywiście i tutaj obowiązuje zasada niedokonywania ekstrapolacji i stosowania równania prostej tylko w granicach wyznaczonych skrajnymi punktami pomiarów.

Za cenę pewnej niedokładności, przybliżenia, mogliśmy w opisany wyżej sposób błyskawicznie uzyskać czas pomalowania powierzchni 0,75m², bez dokonywania pomiarów. Cóż z tego, ktoś powie, skoro wynik jest tylko przybliżony. Jak zwykle, „diabeł kryje się w szczegółach”. Pytanie brzmi: jak bardzo niedokładne jest nasze przybliżenie? W odpowiedzi na takie pytanie pomagają nam odpowiednie metody statystyczne. W praktyce zwykle mamy do czynienia z akceptowalnymi poziomami dokładności.

W przykładzie z malowaniem mówiliśmy o zależności wielkości objaśnianej (czasu) od jednej wielkości objaśniającej (powierzchni). W praktyce nie zawsze tak bywa. Czas pokrywania powierzchni klejem będzie zależał nie tylko od wielkości powierzchni ale też od jej rodzaju i rodzaju kleju. Czas na podjęcie podzespołu będzie zależał od jego ciężaru i wymiarów (warto rozpatrywać te wielkości osobno wszędzie tam, gdzie duże wymiary nie będą zawsze oznaczać automatycznie dużego ciężaru, np. raz podejmowane są podzespoły z litego drewna, a raz z pianki). Zależność nie musi też zawsze mieć charakteru liniowego. W takich przypadkach mówimy o regresji wielorakiej i nieliniowej i, chociaż jest to nieco bardziej skomplikowane niż w naszych przykładach, nadal możemy konstruować modele przydatne do przewidywania wartości wielkości objaśnianych.

Podsumowanie – jak być bardziej efektywnym specjalistą normowania czasu pracy?

Dzięki analizie regresji możemy uzyskiwać normy czasu pracy bez dokonywania pomiarów czasu. Zwiększa to naszą efektywność. Pamiętajmy o tym, jeśli np. będziemy normować aktualną produkcję. Postępując według poniższego schematu możemy wyniki pomiarów wykorzystać w przyszłości dla nowych wyrobów wprowadzanych do produkcji.

1. Ustalamy wszystkie wielkości wpływające (objaśniające) na czas pracy przy aktualnie wytwarzanych wyrobach,
2. dokonujemy pomiarów czasu operacji produkcyjnych, zapamiętując każdorazowo dla jakich wartości wielkości wpływających został zmierzony dany czas,
3. w oparciu o odpowiednie metody statystyczne opracowujemy normy czasu dla aktualnie wytwarzanych wyrobów,
4. na bazie wyników uzyskanych w poprzednim kroku ustalamy zależności funkcjonalne czasu operacji od wielkości wpływających i weryfikujemy statystycznie ich jakość,
5. w przypadku uzyskania satysfakcjonujących wyników weryfikacji statystycznej korzystamy z funkcji określonych w kroku poprzednim do ustalania czasów pracy dla wyrobów nie objętych wcześniej pomiarami (np. dla nowego asortymentu), podstawiając do funkcji wartości wielkości wpływających dla tych wyrobów.

Oczywiście o zwiększonej efektywności będziemy mówić wtedy, jeśli czas na ustalenie wielkości wpływających, zapamiętywanie ich wartości dla bieżącej produkcji i określanie zależności statystycznych nie będzie dłuższy niż pomiary dla nowych wyrobów. Dla spełnienia tego warunku warto rozważyć wsparcie w postaci dostępnego na rynku, wyspecjalizowanego oprogramowania komputerowego.

Leszek Nowaczyk

Autor jest doradcą i trenerem certyfikowanym przez REFA Bundesverband e.V. Prowadzi projekty w obszarze organizacji pracy i zarządzania, w tym projekty z wykorzystaniem specjalistycznego oprogramowania do normowania czasu pracy.